五年生の学習した体積の公式 直方体・・・たて ×横 高さ ・立方体の体積・・・ 一辺× 6 本単元においてめざす児童像 資 質 ・ 能 力 目 指 す 児 童 像 思考力・表現力 角柱や円柱の体積の求め方を理解し,必要な部分の長さを用いて 多角柱の体積について,図形を用いて説明することができる 円柱の体積=7×7×314×12=(cm³)となります。 答え 円柱ができる。 体積はcm³ ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積 五面体の捉え方(都立新宿) 空間幾何 小学生~中2生対応可能 都立 (神奈川県立)入試問題 多面体の体積は、 「その立体をどう捉えるか」 によって簡単に求められたり、逆に面倒になったりします。 世の中の出来事を、 「多様な面から捉える力

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
五角柱の体積の求め方
五角柱の体積の求め方- その長方形を縦に積み重なったものの体積を求めているのですから、高さをかければ良いということです。 他にも、1c㎡のブロックが何個あるのかという考え方をしてみるのも分かりやすいです。 角柱・円柱の体積の公式をチェック 三角形、四角形、五角形・・・などの多角形が積み重 *グラフ上の三角形の面積の求め方は、記事内の「座標の指導案(応用)」の章で解説しています。 練習問題 では錐の体積の練習問題です。 問題3は長崎県の公立高校入試問題。19年度の大問4の13をそのまま載せます。



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
式ア 角柱及び円柱の体積の求め方を考えること。 (4) 速さについて理解し,求めることができるようにする。 (5) メートル法の単位の仕組みについて理解できるようにする。 c 図形体積 角柱または円柱の底面積をS、高さをh、体積をVとすると、 = と 「皆さんどうも!今回は初めての授業ノート公開です!(o´Д`)緊張しますが良ければコメント、フォロー等よろしくお願いします!(*´ω`*) ちなみに余談ですが主は最高でも黒と赤と青しか基本使わない主義です。(大事なところが分からなくなってしまう)」, キーワード 算数,小6,角柱の体小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 図形の拡大と縮小拡大図と縮図 問題プリント 小学6年生の算数図形の拡大と縮小
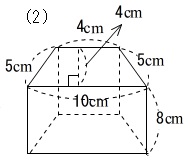
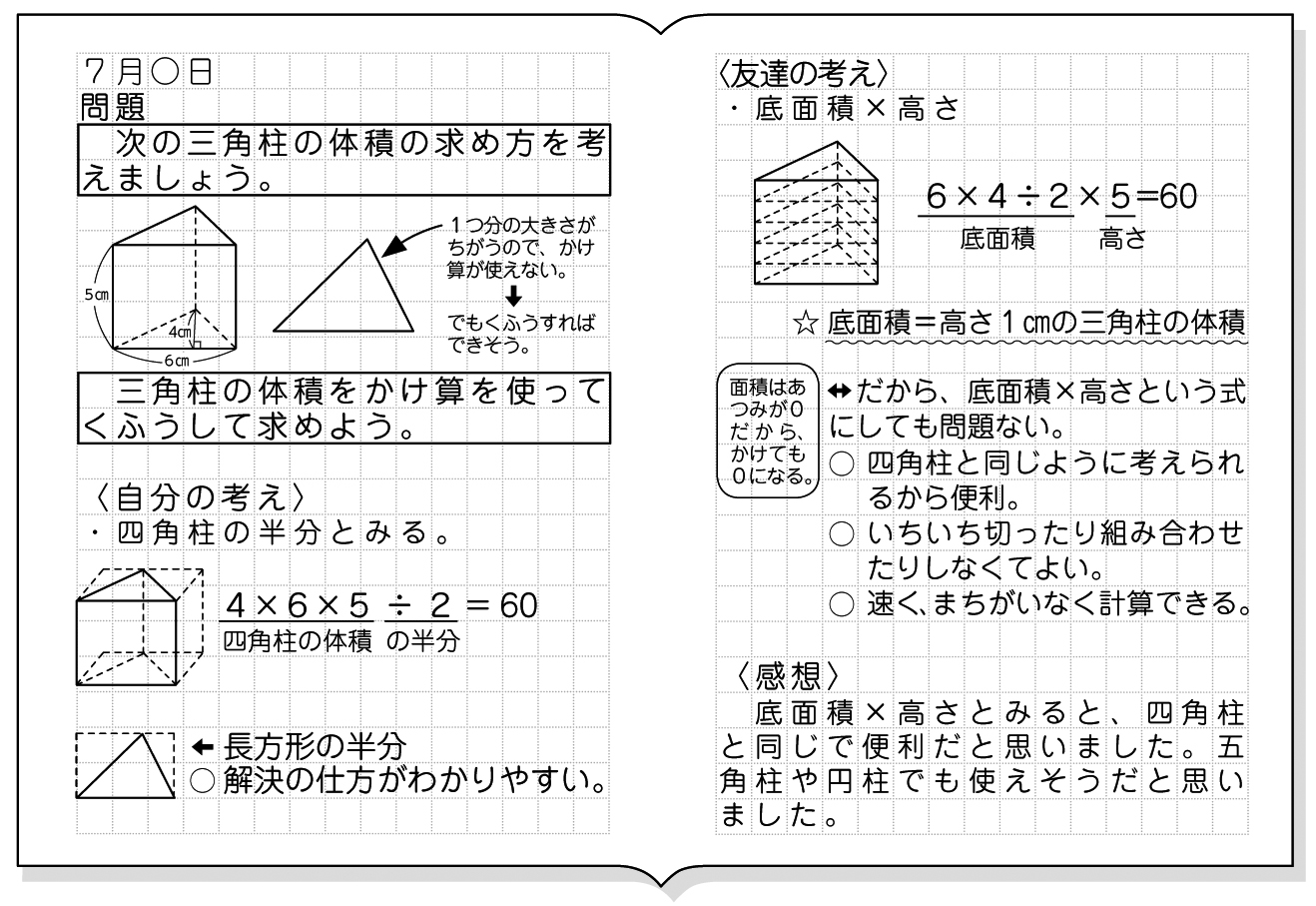
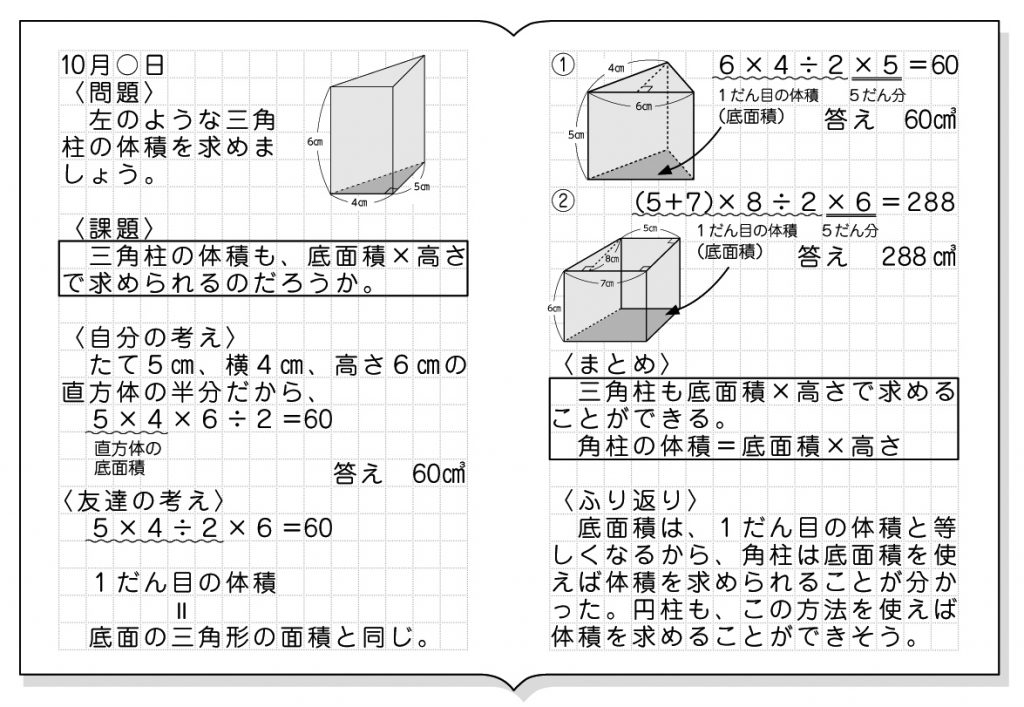
の体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方 角柱の体積=底面積×高さ 評価問題 次の体積を求め、そのわけを説明しましょう。 子供に期待する解答の具体例 ①6×4÷2×5=60 60㎤ 「ここに三角形の底面積と同じ体積の1段目ができて、それが5段積み上がるから、6×4÷2×5で求められます。 」 ②(57 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、
対辺、高さから計算 A : H : 体積: 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい 四角すい 多角形 6角柱 六角角柱の体積も同様に求められること,さらには,どんな角柱でも三角柱に分割できること,角柱の底 面の辺の数を増やしていくと円柱に近づくと拡張していくことで,一般の角柱・円柱の体積の求積公 式を「底面積×高さ」とまとめることができる統合的な考え方を育てたい。 その際,三角柱6角柱 六角柱 対辺 体積計算 公式 求め方 高さ 自動 volume 体積 6角柱 六角柱 面積;
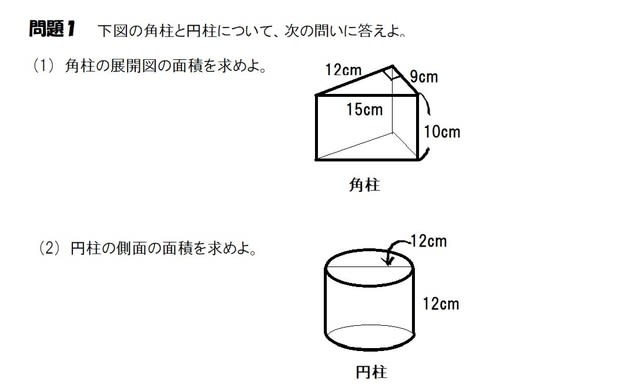



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support



6年算数 円柱と角柱の体積 教え方2
四角錐台の体積 110 /192件 表示件数 5 10 30 50 100 0 1 11 30歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 調整池容量確認 ご意見・ご感想 とても役に立ちました。 今回は、四角錐(しかくすい)の体積の求め方(公式)について書いていきたいと思います。 四角錐の体積の求め方公式 四角錐の体積を求める問題 問題① 《四角錐の体積の求め方》 問題② 《四角錐の体積の求め方》 問題③ 《四角錐の高さの求め方》 (adsbygoogle = windowadsbygoogle角錐の体積、角柱の体積の違いを下記に示します。 角錐の体積 ⇒ 底面積×高さ×3分の1 角柱の体積 ⇒ 底面積×高さ 角錐の体積が柱体の3分の1になる理由 下図の角錐をみてください。角錐の底面は三角形ですが、分かりやすく示しただけで底面積は任意の値aとします。角錐の頂点の位置が0の




角柱 円柱の表面積と体積の公式 数学fun
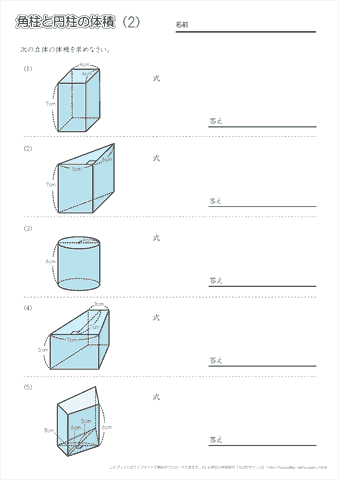



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
教え方4 角柱の体積の求め方の考え を使って、 円柱の体積の求め方 を考えさせます。 動画作成協力・・ 動くイラストフリー素材 上の図のように、円柱の中に入る角柱の底面の辺の数 (多角形の角の数)を増やしていくと円柱になることが考えられます 台形の面積公式や、ひし形の面積の求め方など、覚えておかなければいけないことがいくつかあったと思います。しっかりと復習をしてください。 四角柱の体積を求める問題 問題 底面積の四角形が上底が2㎝、下底が4㎝、高さが2㎝の台形で、それを底面積とする四角柱の高さ角柱の体積は?公式と求め方 角柱の体積の公式は 底面積×高さ です。ただし角柱には三角柱や四角柱など色々な種類があります。角柱の種類ごとに底面の形状が違うので、底面積の公式も変わります。 とはいえ難しく考える必要は無いです。三角形、四角形、台形、円形など基本的な図形の




体積の求め方 計算公式一覧




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
という「角柱の体積の公式」を使っているだけなんだ。 今日はこの公式をわかりやすく解説していくよ。 よかったら参考にしてみてね! 三角柱の体積の求め方がわかる2つのステップ 三角柱の体積は2ステップで計算できちゃうんだ。 つぎの例題をときながら求め方を確認していこう。 三 →角柱の体積 →円柱の体積 →いろいろな体積(しばらくお待ちください) 古いプリント 角柱の体積1 基本的な角柱の体積の 角柱の体積の求め方を考える授業では、絶対に授業者が忘れてはならない大前提の考えがあります。それは、 角柱の体積は、底面積×高さ で求められるかどうかは解説 角柱,円柱の体積 底面積が ,高さが の円柱や角柱(三角柱,四角柱,五角柱,・・)の体積 は, (底面積×高さ) で表わされます。 特に円柱では,底面の半径をrとすると だから になります。




角柱の体積を求める 5つの方法 Wikihow




小5 角柱と円柱 小学生 算数のノート Clearnote
角柱や円柱、円錐などの体積の求め方を解説しています。 中学受験のための算数塾 中学受験に必要な算数の基本テクニックを紹介しています。中学受験算数の独特な解法は、小学校では教わらない「裏技」的なものが多いので注意が必要です。 例題を使って、コツやポイントを押さえながら今回の記事では四角柱の体積・表面積の求め方について、 サクッと解説していきます(^^) 難しい説明などは省いて、問題を解けることを優先しております。 この記事を読みながら手元の宿題やワークを一緒に解き進めていきましょう。 Contents 四角柱の体積;立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm



3
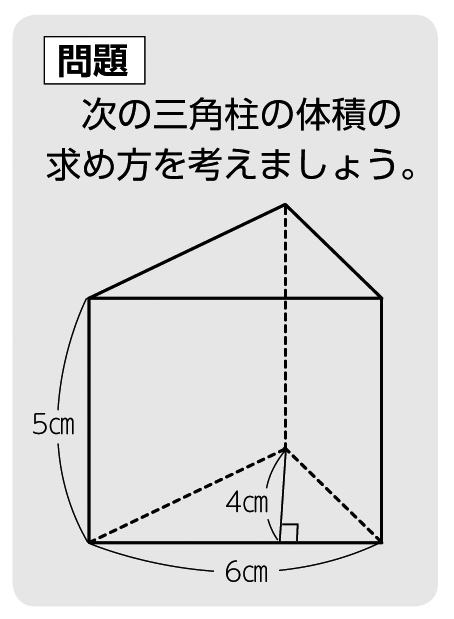



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術
中学1年生 中学校数学 角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 中学1年生で習う空間図形には、様々な立体の体積 角柱と円柱の底面積と体積の求め方を教えて下さい 4角柱⤵︎⤵︎⤵︎ ①体積が105cm3で、高さが6cm4角柱の体積は何cmですか。 式 答え ⤵︎⤵︎⤵︎円柱 ②体積が945cm3で、底面積が785cm2の円柱の高さは何cmですか。 式 答え角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



2
三角柱の体積と表面積 三角柱は小学6年生のときに習います。 しかし、 三角柱の体積・表面積 は高校入試にも大学入試にも出題されるとても重要な単元です。 求め方や公式はとても単純でわかりやすいものなので、基礎知識はこれを機にしっかり押さえましょう!2 角柱の体積の求め方を考え,求めるこ 考三角柱の体積の求め方を,底面 とができる。 積×高さの式を基に図や式を用 ・四角柱の体積の求め方を基にして, いて考え,式や図への書き込み, 三角柱の体積の求め方を考える。 言葉で表現している。6 角柱と円柱の体積 ・底面積の意味 ・角柱、円柱の体積の求め方 と公式 6 指導と評価の計画(全10時間) 次 時 主な学習内容 主な言語活動 評価 関 考 技 知 主な評価規準(評価方法) 第 一 次 も の の か さ の 表 し 方 1 (本 時 ) ・ 2 ・液体の体積や
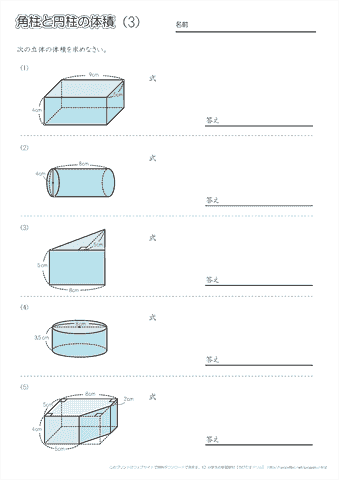



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




小5 算数 小5 60 角柱と円柱 Youtube
①直方体・立方体の体積 p17 1 p18 1 p 1 ②大きな体積 p21 1 p21 3 ③容積 p22 1 p22 2 p23 1 ④体積の単位の関係 p24 1 ③比例 p29~30 1 p31 3 ④小数のかけ算 ①整数×小数 p35 1 p36~37 2 p38 1 p38~39 2 ②小数×小数 p40 1 p40 2 p41 1 p41 2 p42 5 p42 7 ③小数のかけ算を使って p44~45 1 p46 1 p47 2 ④




立体の体積の求め方 何角柱でも何角錐でも同じ




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球



5年算数角柱と円柱 2 いっちに算数 わかる教え方



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術




算数図形編 立方体 直方体 角柱 角すい 展開図をうまく活用しよう 中学受験 高校受験パスナビ




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット



小学6年生 算数 無料問題集 角柱や円柱の体積 おかわりドリル




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




6年算数 立体の体積 のわかる教え方 いっちに算数 のブログ




体積の求め方 計算公式一覧



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




角柱の体積を求める 5つの方法 Wikihow




角柱と円柱の体積の求め方を解説してください 答えは459cm3です Clearnote



答え合わせをお願い致します 数学1図形の問題です 問題下の図の五角柱の面 Yahoo 知恵袋




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット



右の図は 五角形を底面とする角柱です この角柱の体積を求めなさい Yahoo 知恵袋




角柱 円柱の表面積と体積の公式 数学fun




角柱の体積 Youtube



正六角柱の体積の求め方を教えてください D ノ 底 Yahoo 知恵袋




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
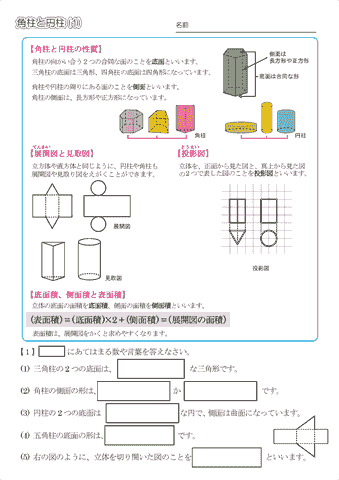



小学5年生の算数 角柱と円柱 問題プリント ちびむすドリル 小学生
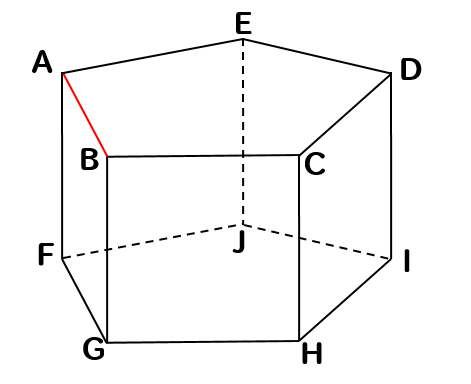



中学数学 ねじれの位置の意味とは 角柱 角錐のどこ 問題を使って解説するぞ 数スタ




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
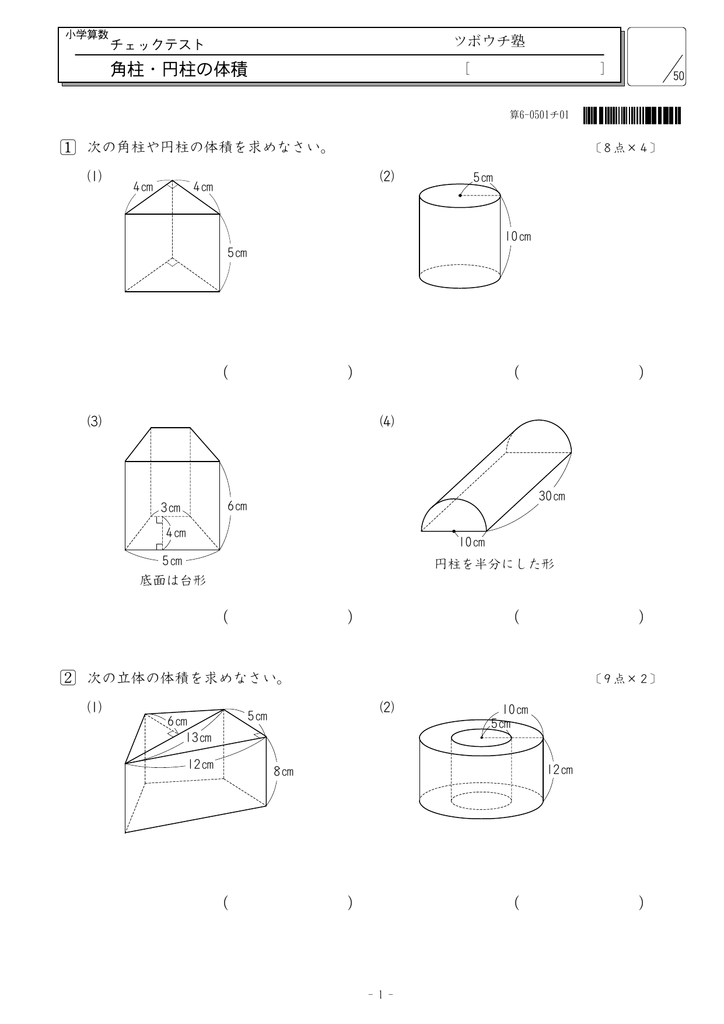



画像 角柱 と 円柱 の 体積 ニスヌーピー 壁紙




5 2 直方体 立方体 柱の体積 算数がわかるようになるページ
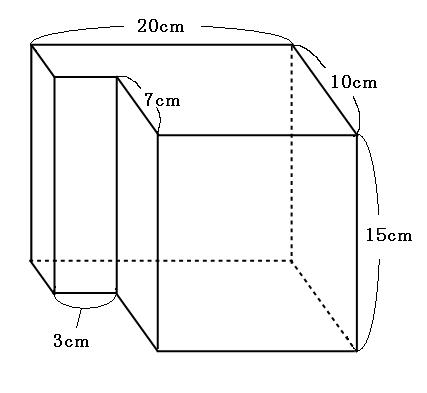



立体の体積の求め方 何角柱でも何角錐でも同じ



3



角柱の体積は 1分でわかる公式 求め方 底面積 台形の関係



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



9月7日 6年生 算数 田殿小学校




反角柱 Wikipedia




体積の求め方ー四角柱ー 小学生 算数のノート Clearnote



2



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
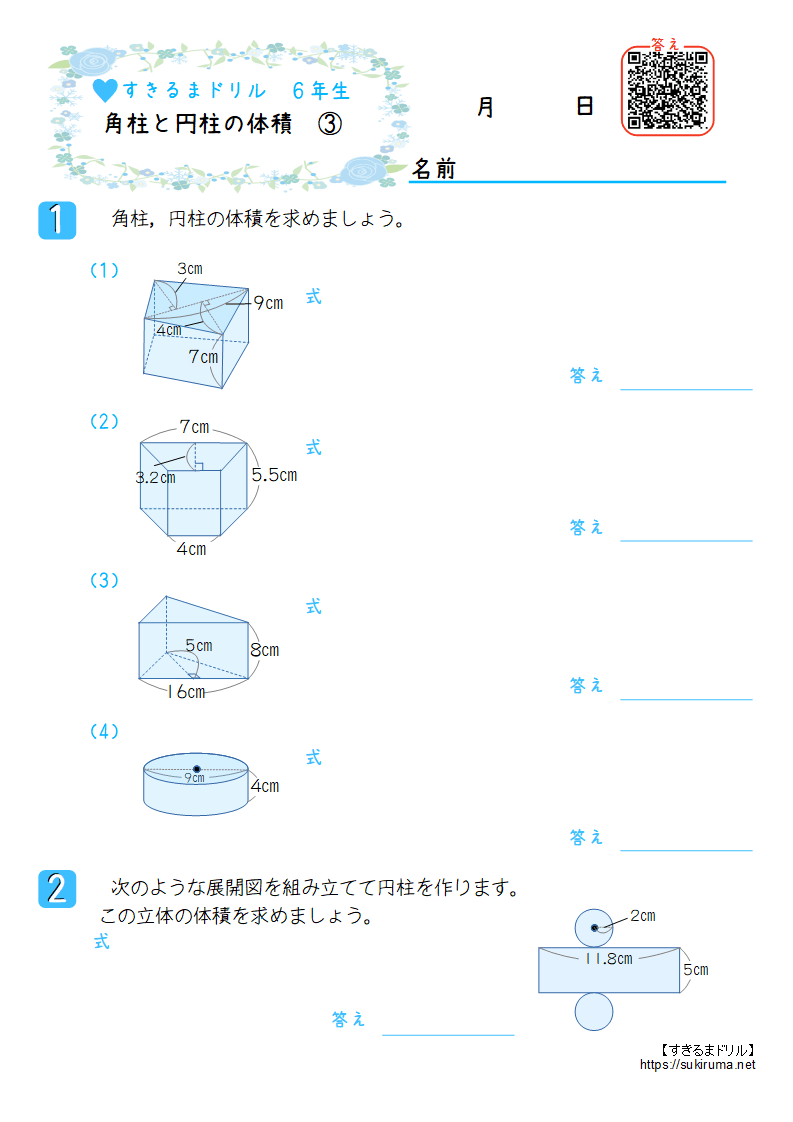



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント



6年算数 円柱と角柱の体積 教え方2




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



6年算数 円柱と角柱の体積 教え方2




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




6年算数角柱と円柱の体積 立体の体積 教え方




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
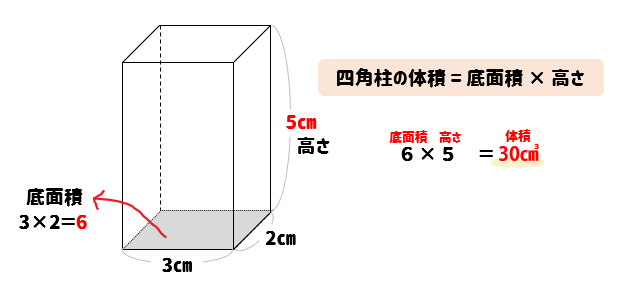



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ
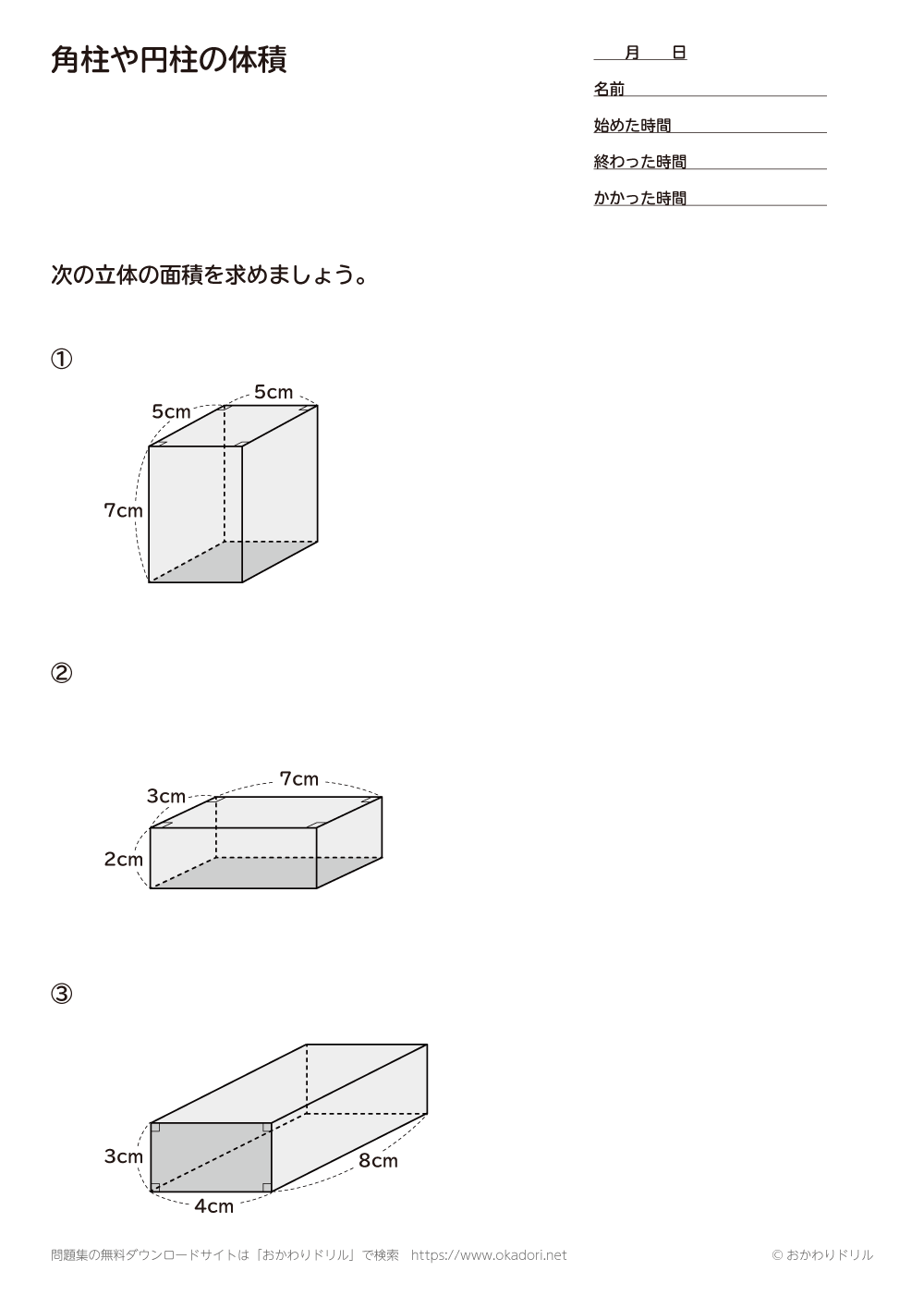



小学6年生 算数 無料問題集 角柱や円柱の体積 おかわりドリル



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




柱体の体積 三角柱 四角柱 五角柱 円柱 S6s09 01 Youtube



1



Studydoctor角柱や円柱の展開図の形 中学1年数学 Studydoctor




4月24日 小5算数 ジャングルジムブログ




5 2 直方体 立方体 柱の体積 算数がわかるようになるページ
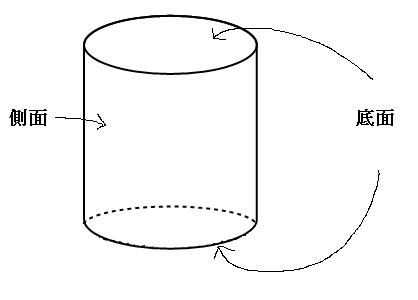



立体の体積の求め方 何角柱でも何角錐でも同じ




多くの教師が失敗する角柱の体積の求め方 算数を究める
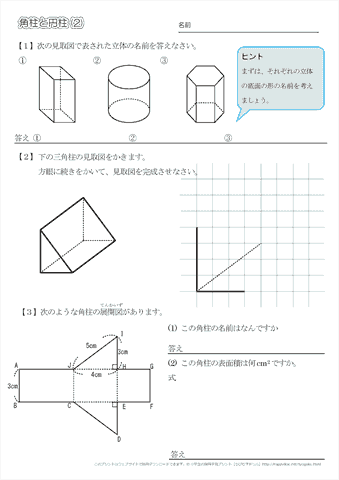



小学5年生の算数 角柱と円柱 問題プリント ちびむすドリル 小学生




角柱の表面積 Youtube




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




四角柱の表面積 数学 この問題の表面積 出題ミスですか Okwave




小5 複雑な立体の体積 直方体 日本語版 Youtube



6年算数 円柱と角柱の体積 教え方2




角柱 円柱の表面積と体積の公式 数学fun




体積 表面積




角柱や円柱の表面積の求め方を教えてください Clearnote
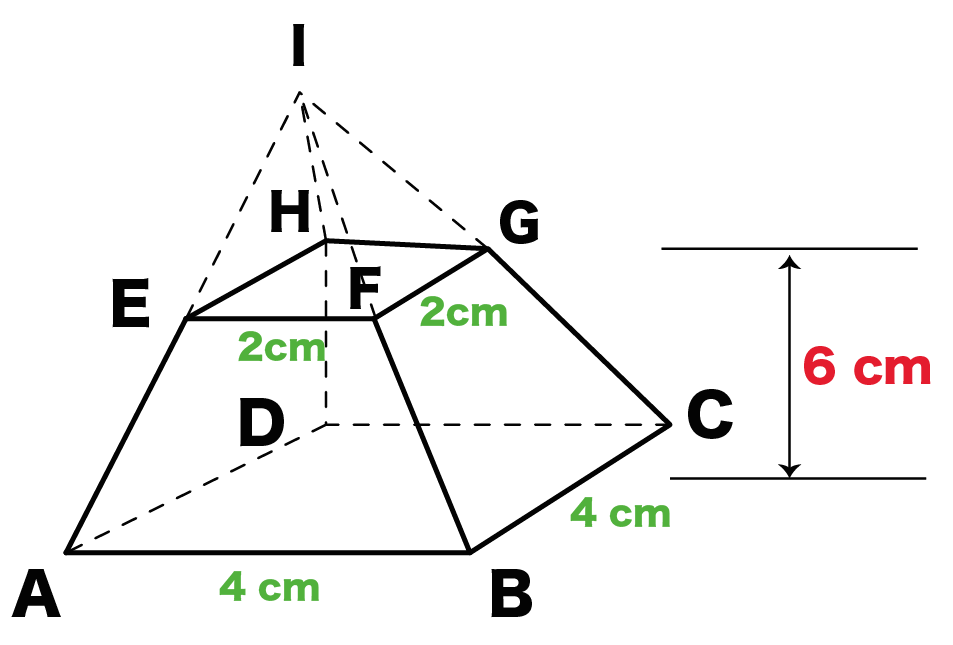



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



わからないので教えていただけるとありがたいです 下 Yahoo 知恵袋



1




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
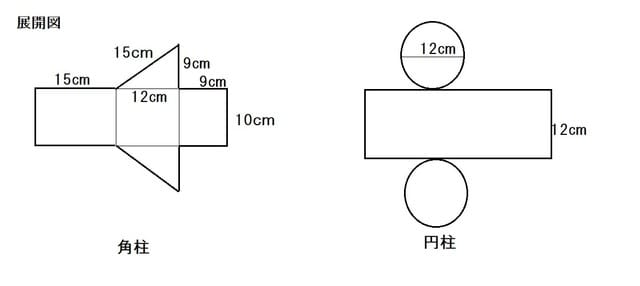



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 小学校 算数




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
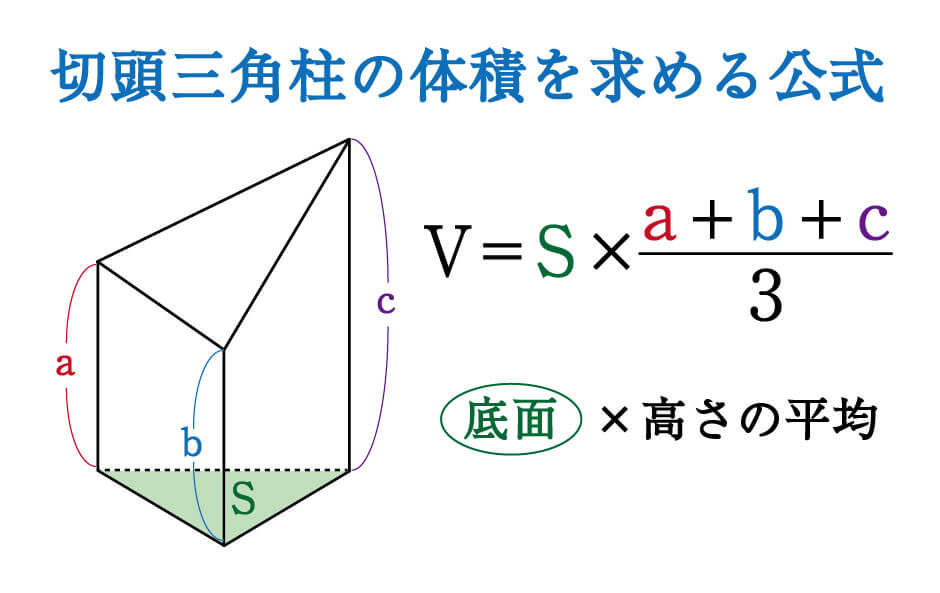



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
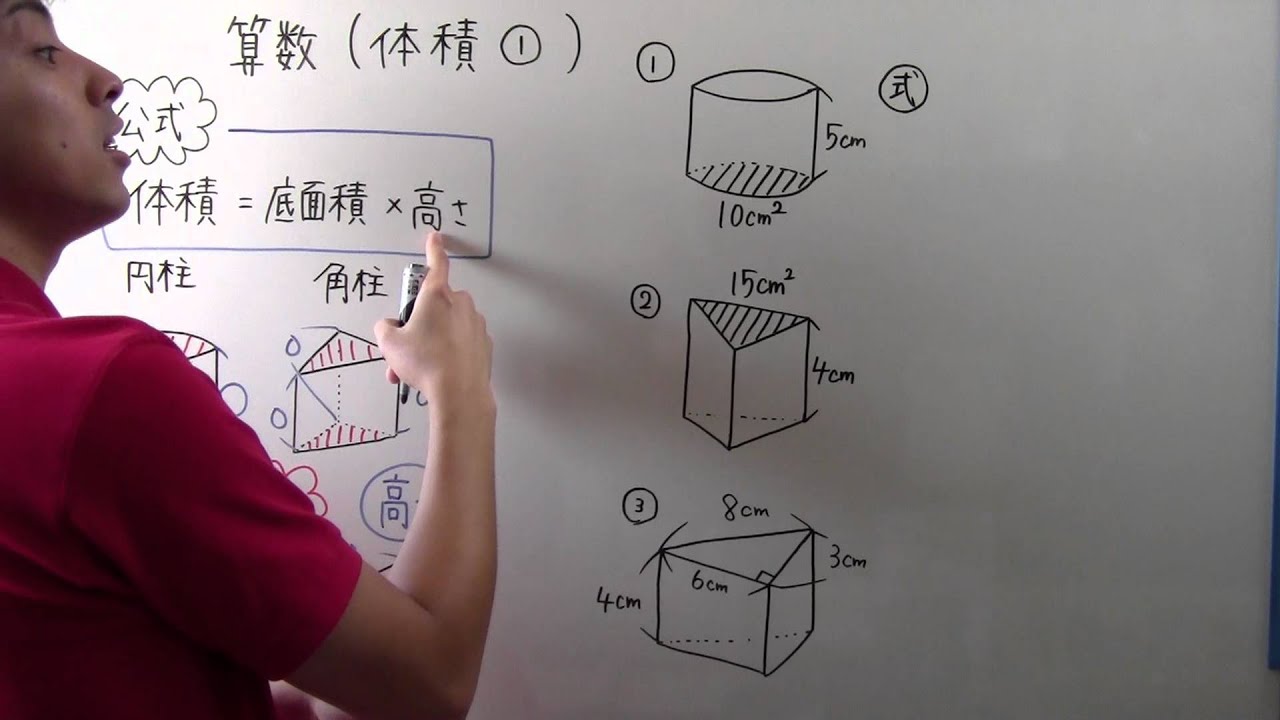



小6 算数 小6 25 体積 円柱 角柱 Youtube
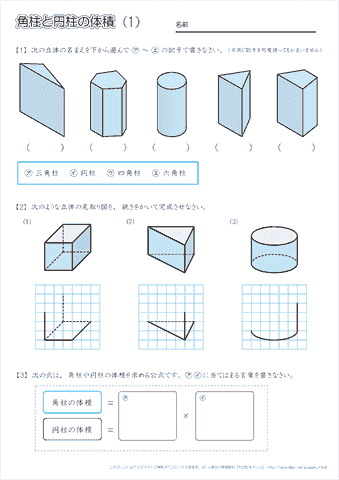



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




教えてください Clearnote




โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clearnote




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
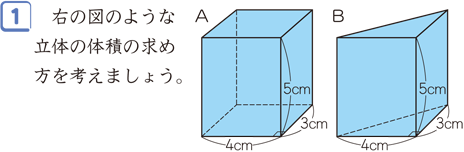



角柱と円柱の体積 算数用語集



6年算数 円柱と角柱の体積 教え方2
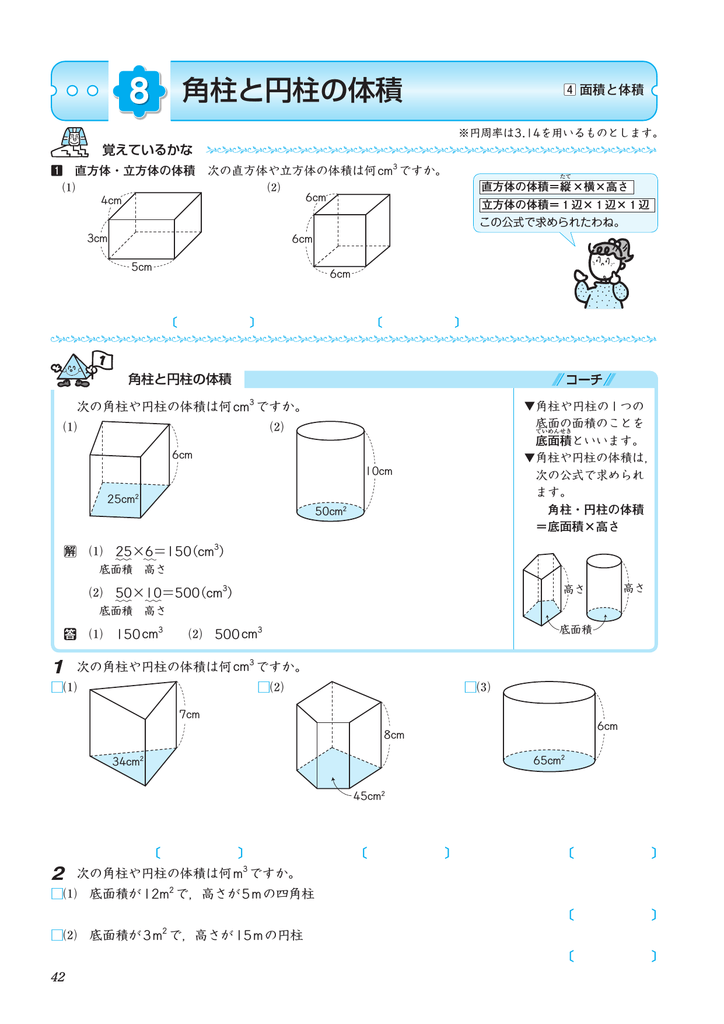



角柱と円柱の体積
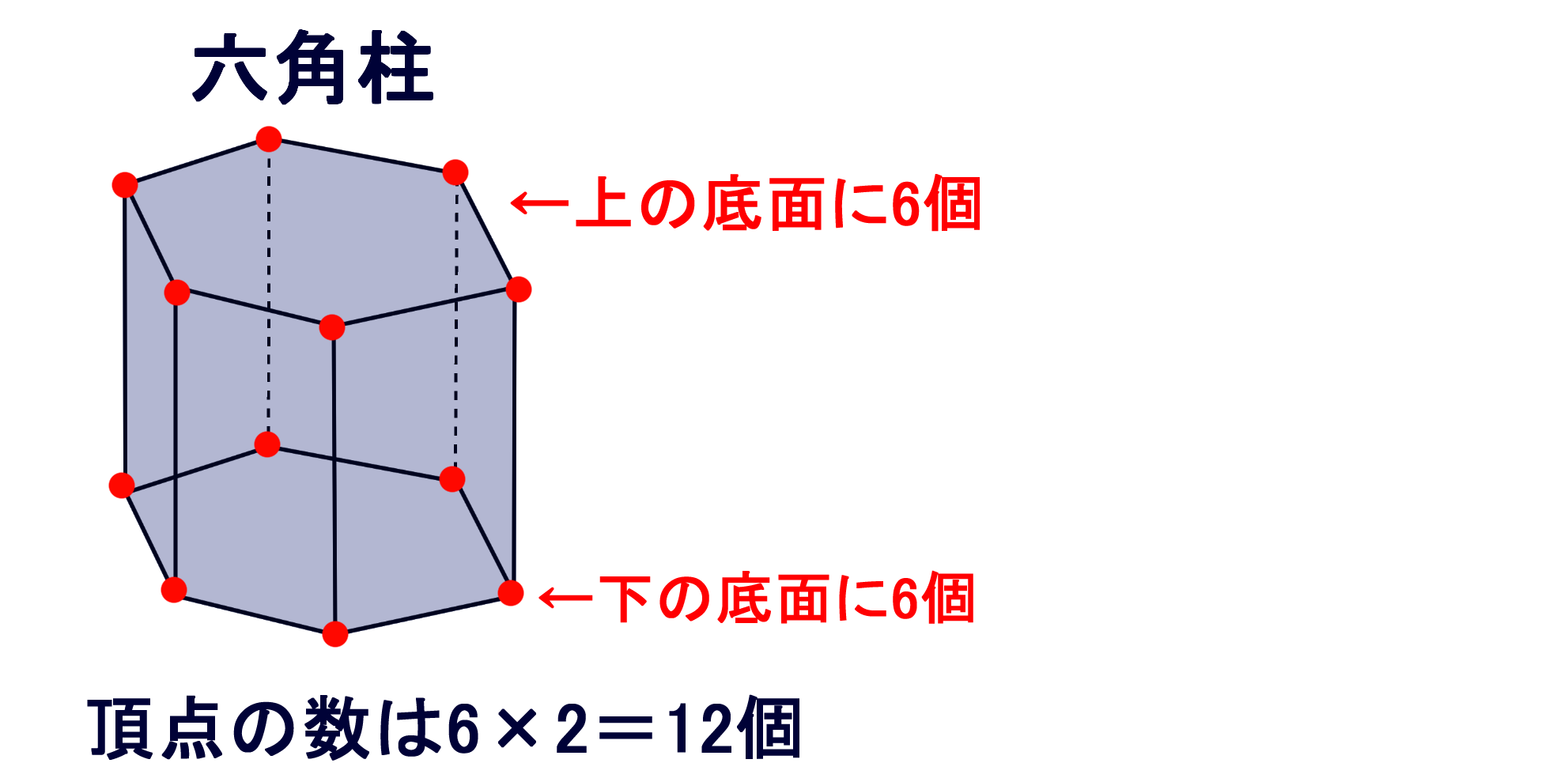



角柱 角錐の辺の数 頂点の数 面の数 バカでもわかる 中学数学




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく


